AutoEncoder
AutoEncoder
概念
AutoEncoder(自动编码器)是一种无监督学习算法,
常用于数据降维和特征提取。它由两个主要部分组成:编码器(encoder)和解码器(decoder),AutoEncoder的目标是尽可能地重构输入数据。训练过程中,AutoEncoder通过最小化重构误差来学习如何有效地编码和解码数据。这可以促使模型学习到数据的有用特征,进而实现数据降维和特征提取的功能。
编码器
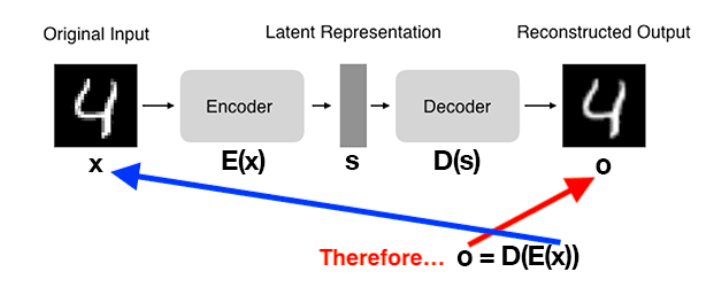
编码器将输入数据映射到一个潜在表示空间(latent space)或代码的低维表示形式。这种潜在空间通常称为嵌入(Embedding),旨在保留尽可能多的信息,允许解码器以高精度重建数据。如果我们将输入数据表示为x ,将编码器表示为 E,则输出潜在空间s表示为s=E(x) 。
解码器
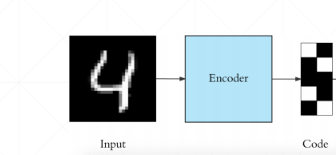
解码器通过接受潜在空间表示s来重建原始输入数据。如果我们将解码器函数表示为D ,将解码器的输出表示为o ,那么我们可以将解码器表示为 o=D(s)。
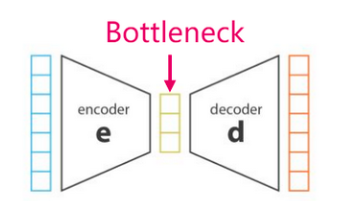
Bottleneck
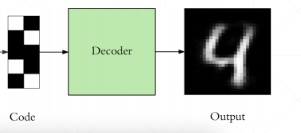
瓶颈层是连接编码器和解码器的中间层,其维度通常比输入和输出的维度要低。这种设计可以强制模型学习到输入数据的更紧凑的表示,提取数据中最关键的特征。因此,瓶颈层起到了降维和抽象的作用,有助于提高模型的表示能力和泛化能力。
瓶颈层的存在也可能导致信息丢失或损失,因为它限制了模型对输入数据的表达能力。因此,在设计模型时需要权衡瓶颈层的维度选择,以平衡降维和信息保留之间的关系。
AutoEncoder实现MNIST
模型
import torch
from torch import nn
from torchsummary import summary
class AutoEncoder(nn.Module):
def __init__(self,in_features,lantent_dim=128):
super(AutoEncoder, self).__init__()
# encoder: in_features->512->256->lantent_dim
self.encoder = torch.nn.Sequential(
torch.nn.Linear(in_features=in_features, out_features=512),
torch.nn.ReLU(),
torch.nn.Linear(in_features=512, out_features=256),
torch.nn.ReLU(),
torch.nn.Linear(in_features=256, out_features=lantent_dim),
)
# decoder: lantent_dim->256->512->in_features
self.decoder = torch.nn.Sequential(
torch.nn.Linear(in_features=lantent_dim, out_features=256),
torch.nn.ReLU(),
torch.nn.Linear(in_features=256, out_features=512),
torch.nn.ReLU(),
torch.nn.Linear(in_features=512, out_features=in_features)
)
def forward(self,x):
# 扁平化为784个神经元
x = x.view(-1, 784)
# encoder部分
x_e = self.encoder(x)
# decoder部分
x_d = self.decoder(x_e)
# 还原为28*28的灰色图像
return x_d.view(-1,28,28)
if __name__ == '__main__':
print(summary(AutoEncoder(in_features=784),(28,28),device="cpu"))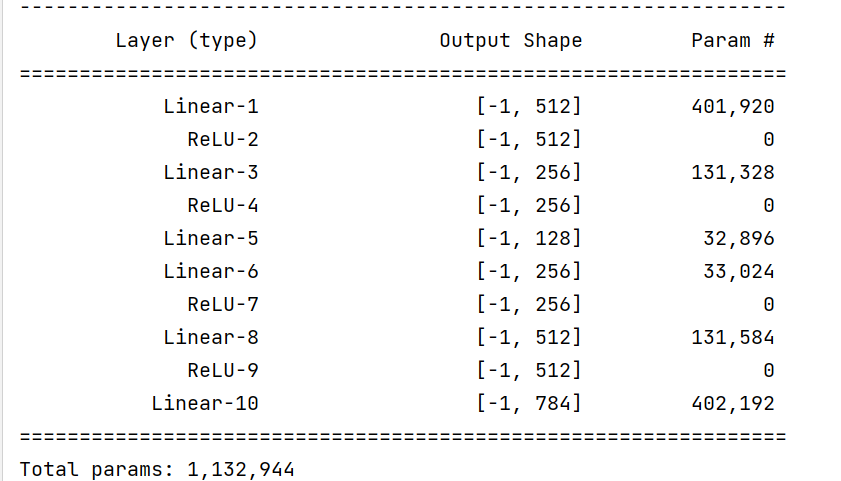
训练
import time
from argparse import ArgumentParser
import torch
import torchvision
from matplotlib import pyplot as plt
from torch.utils.data import DataLoader
from torchvision.transforms import transforms
from models import AutoEncoder
# 训练
def train(args):
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# 预处理
transform = transforms.Compose([
transforms.Resize(size=(28, 28)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.5], std=[0.5]),
])
# 下载数据集
train_dataset = torchvision.datasets.FashionMNIST(root=args.TRAIN_DATA, train=True,
transform=transform, download=True)
val_dataset = torchvision.datasets.FashionMNIST(root=args.VAL_DATA, train=False,
transform=transform, download=True)
# 加载数据集
train_loader = DataLoader(dataset=train_dataset,batch_size=args.BATCH_SIZE,shuffle=True,num_workers=args.NUM_WORKERS)
val_loader = DataLoader(dataset=val_dataset,batch_size=args.BATCH_SIZE,shuffle=True,num_workers=args.NUM_WORKERS)
# 加载模型
auto_encoder = AutoEncoder(in_features=784).to(device)
# 定义损失函数和优化器
loss_fn = torch.nn.MSELoss()
optimizer= torch.optim.Adam(auto_encoder.parameters(), lr=args.LEARNING_RATE, betas=args.BEATAS)
# 训练集总loss列表
train_loss_all = []
# 验证集总loss列表
val_loss_all = []
# 迭代epoch
for epoch in range(args.NUM_EPOCHS):
# 保存开始时间
start = time.time()
print(f"epoch {epoch}/{args.NUM_EPOCHS - 1}")
print("-" * 10)
# 初始化训练集的loss
train_loss = 0.0
# 初始化验证集的loss
val_loss = 0.0
# 训练过程
for step, (imgs, _) in enumerate(train_loader):
# 放入GPU中
img, _ = imgs.to(device), _.to(device)
# 将模型设置为训练模式
auto_encoder.train()
# 前向传播
output = auto_encoder(img)
# 计算损失值
loss = loss_fn(output, img)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 对损失函数累加loss值
train_loss += loss.item()
# 验证过程
for step, (imgs, _) in enumerate(val_loader):
img, _ = imgs.to(device), _.to(device)
# 设置模型为评估模式
auto_encoder.eval()
# 前向传播
output = auto_encoder(img)
# 计算损失值
loss = loss_fn(output, img)
# 对损失函数累加loss值
val_loss += loss.item()
# 保存每一次epoch迭代的训练集、验证集的loss值、准确率
train_loss_all.append(train_loss/len(train_loader))
val_loss_all.append(val_loss/len(val_loader))
end=time.time()
# 打印每个epoch列表叠加后的最后一次值
print("{} Train Loss: {:.4f},use:{:.1f} minutes".format(epoch, train_loss_all[-1],(end-start)/60))
print("{} Val Loss: {:.4f},use:{:.1f} minutes".format(epoch, val_loss_all[-1],(end-start)/60))
plt.plot(range(1, args.NUM_EPOCHS+1), train_loss_all, label='train_loss',color="red")
plt.legend()
plt.plot(range(1, args.NUM_EPOCHS + 1), val_loss_all, label='val_loss',color="blue")
plt.legend()
plt.title('AE-LOSS')
plt.show()
if __name__ == '__main__':
parser = ArgumentParser()
# 形参名以--xx开头
parser.add_argument("--BATCH_SIZE", default=128)
parser.add_argument("--LEARNING_RATE",default=0.001)
parser.add_argument("--NUM_EPOCHS",default=20)
parser.add_argument("--BEATAS",default=(0.5,0.999))
parser.add_argument("--TRAIN_DATA",default="./data")
parser.add_argument("--VAL_DATA",default="./data")
parser.add_argument("--NUM_WORKERS",default=8)
# 解析命令行参数
args, _ = parser.parse_known_args()
# 训练
train(args)20轮效果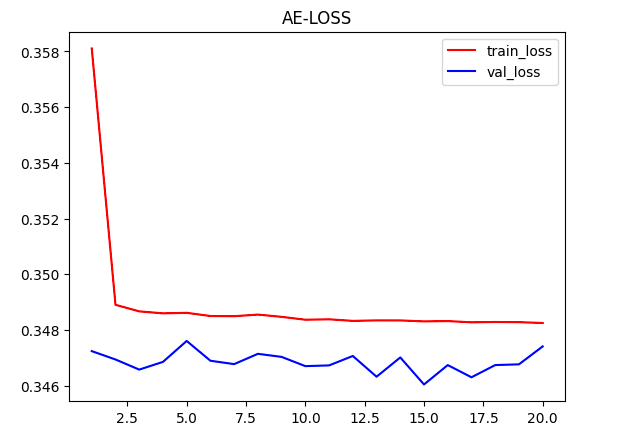
Denoising AutoEncoder
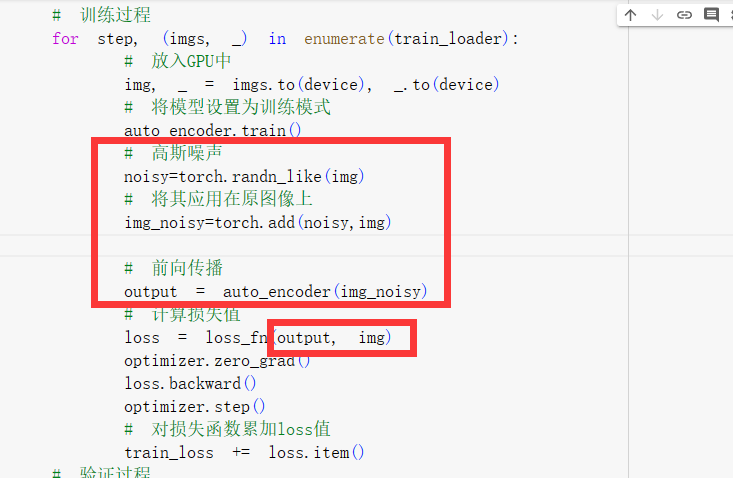
去噪自动编码器:在输入数据上添加一个高斯噪声,使模型重构原始的数据,学习数据真正的分布,而目标仍然是原始的、未损坏的数据。自动编码器学习从噪声输入中重建干净的数据,使其可用于图像去噪和数据预处理任务。
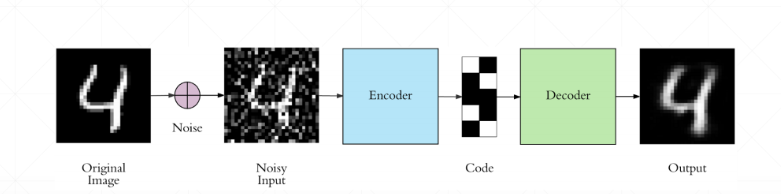
实现
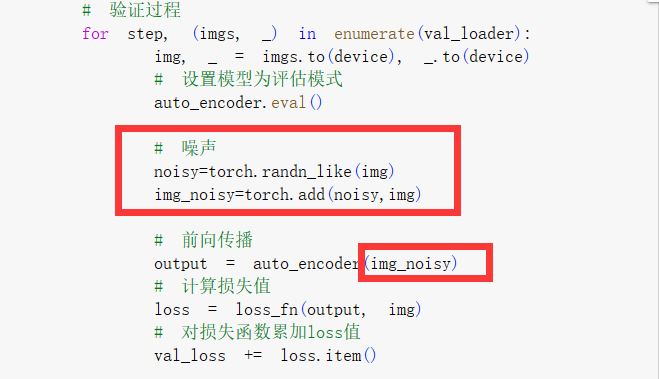
同AutoEncoder的代码,只是在训练和验证阶段需要将原始图片加上高斯噪声后传入模型中
Dropout AutoEncoder
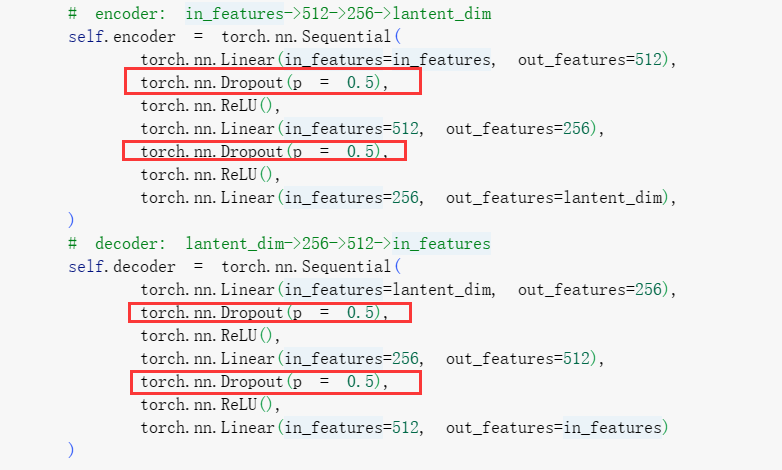
在传统的自编码器中,编码器将输入数据映射到一个较低维度的隐藏表示,然后解码器将隐藏表示映射回重构的输入数据。而在Dropout AutoEncoder中,我们在编码器和解码器的过程中应用dropout操作。
实现
同AutoEncoder的代码,只是在encoder和decoder中加入了dropout操作
Variational AutoEncoder
VAE的核心思想:编码器将输入数据映射到潜在空间Z中,并且通常将这个潜在空间建模为一个高斯分布N(μ, σ^2)。这个分布的均值μ和方差σ是由编码器输出的,通过 z = μ + σ ∗ ε 将一个标准正态分布的噪声ε通过线性变换和非线性变换映射到了高斯分布 N(μ, σ^2) 上 ,然后从潜在空间中采样多个 z,并通过解码器将其映射为重构输出 x',我们可以得到一组重构样本,从而近似地反映出输入数据 x 的分布特征。
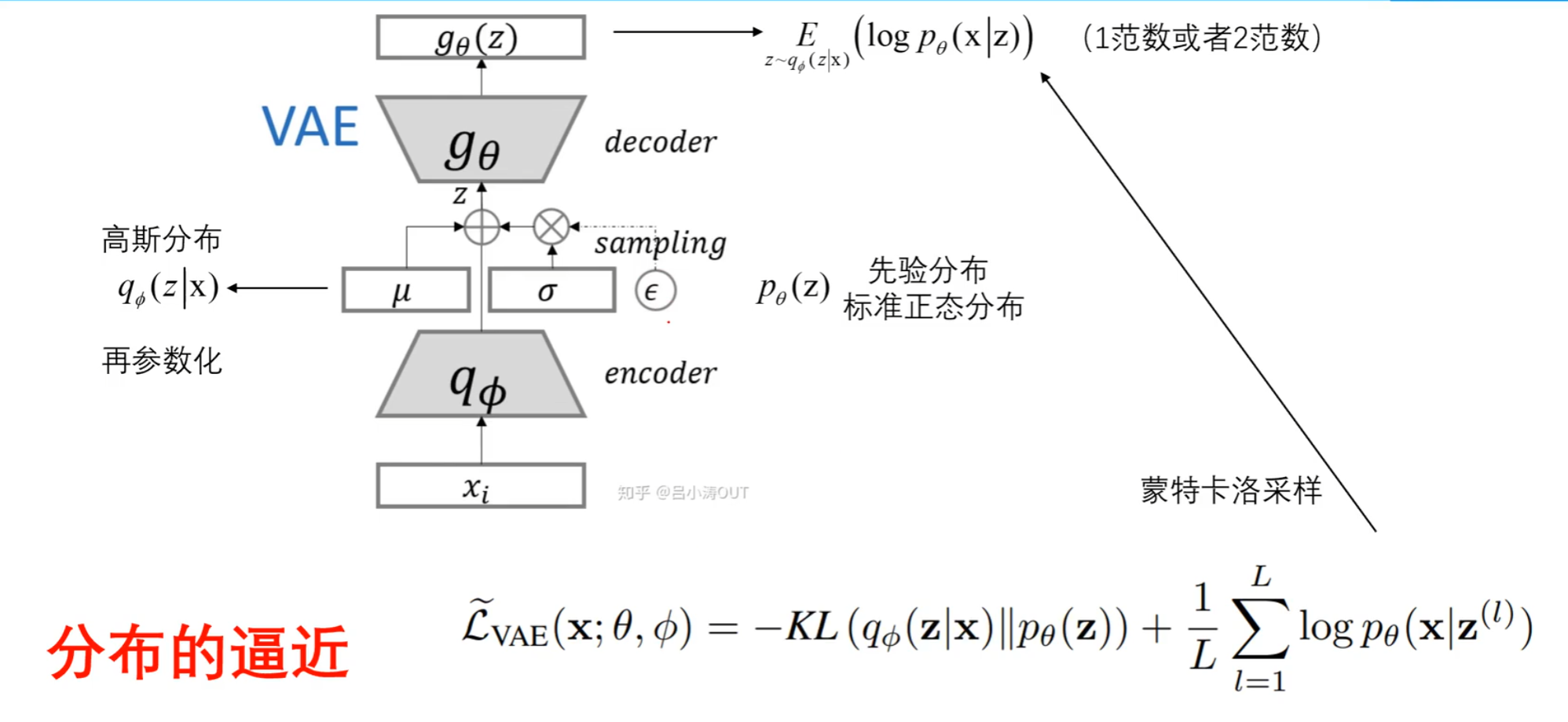
后验分布
在VAE中,后验分布是通过编码器网络(Encoder)计算得到的。它将输入数据映射到潜在空间的均值和方差参数,从而定义了一个多元正态分布。这个多元正态分布描述了给定观测数据后,潜在变量的不确定性。
如何采样
正态分布的线性性质:如果 X ~ N(μ1, σ12) , Y ~ N(μ2, σ22),则 aX + bY ~ N(aμ1 + bμ2 , a2σ12 + b2 σ22),其中 a 和 b 是常数
- μ:后验分布得到的均值
- σ:后验分布得到的方差
- n:先验分布得到的标准正态分布
# 省略上面部分:获取encoder中的均值与方差
μ, σ = torch.split(stats, self.out_channels, dim=1)
# 先验分布:标准正态分布,生成了一个N(0, 1)的正态分布
n=torch.randn_like(μ)
# 重参数化采样技巧: 得到(μ, σ^2)的正态分布
z = μ + n *σ注意:这里n*σ得到的是N(0, σ^2) 的标准正态分布(其中σ~N(0,σ^2) ,n~N(0,1)),最后加上 μ得到的张量就是 N(μ,σ^2) 的正态分布
重参数化
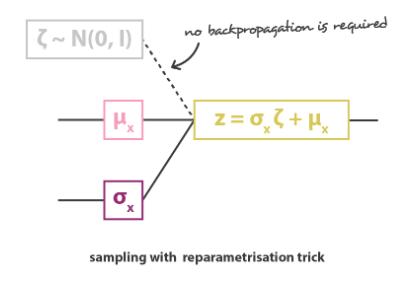
- 在 VAE 中,Encoder生成的潜在表示是一个概率分布,然后再从这个概率分布中进行随机采样,通过Decoder生成数据,这个随机采样操作本身是不可导的,也就不能进行反向传播和梯度下降等优化方法来更新参数。
- 为了解决这个问题,重参数化技术被引入,具体来说,对于VAE模型,编码器网络会输出两个参数,一个表示均值μ ,另一个表示标准差σ 。然后从标准正态分布中随机采样一个噪声值 ε 。然后通过 z = μ + σ ∗ ε 将采样操作转为了一个可微的函数,这样也就使得从潜在分布中采样的过程成为可导的操作,允许梯度通过这个操作传播回编码器,进而进行模型参数的优化。
损失函数
KL loss
KL损失促使潜在分布接近预设的先验分布(即标准正态分布)
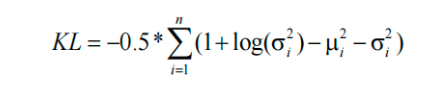
如果复杂分布P(x)是一个具有均值μ和方差σ²的分布,而高斯分布Q(x)的均值为μ₀和方差为σ₀²
则KL(P || Q) = -0.5 * (1 + log(σ₀² / σ²) - (μ - μ₀)² / σ₀² + σ² / σ₀²)Reconstruction loss
让 decoder 的输出X_hat 和输入X 尽可能相似
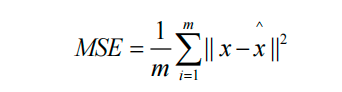
总损失ELBO